

Think about a volume of gas in a container at a constant temperature. The molecules of gas are in random motion. This means that they are flying all over the place at a variety of speeds and in a variety of directions. Each time they hit the walls of the container they exert a force on the wall and the millions of impacts on the walls every second is what causes the pressure of the gas.
If the volume of the gas is decreased the molecules will hit the walls more often and so the pressure of the gas will increase. In fact if we reduce the volume to half the original volume then the molecules will hit the walls twice as often and the pressure of the gas will be doubled. Reducing the volume to one quarter of the original will increase the pressure to four times the original.
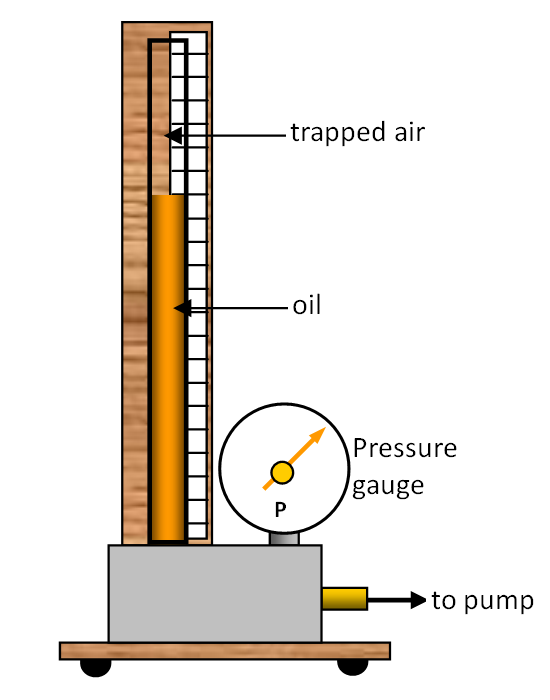
We can
study the behaviour of a gas as we alter the pressure using the apparatus shown in the
diagram.
Some air is trapped in a tube by a column of oil. The oil can be forced up
the tube using the pump and so the pressure of the trapped air can be increased and its
volume decreased.
If we do the experiment slowly so as not to increase the temperature
of the gas then we find that we get the sort of results already suggested.
In fact if you
multiply the pressure of the trapped air at any moment by its volume then this number will
stay constant.

The following two graphs show (a) the variation of pressure with volume (at a constant temperature) and (b) the variation of pressure with rpressure x volume.
